The New Adventures of Curve Pitch Correction
Roger and I have been discussing refinements to the D-Lev pitch correction, and these conversations have really helped me to better understand what it should and shouldn't be doing. Experiments with some new ideas over the past couple of days have produced a design that I'm much happier with in terms of performance and basic functionality. Some recent history:
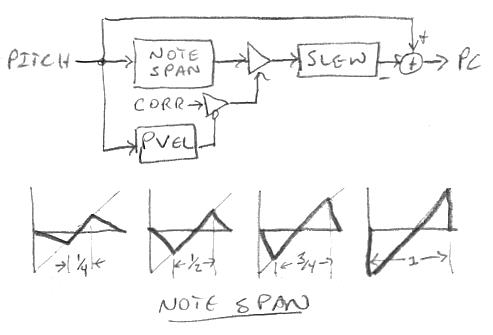
At top is a high level view of the previous pitch correction. The pitch number comes in and is separated into individual notes, which are treated equally by the note span knob (see next). The span amplitude is controlled by the corr knob, which itself is modulated downward by the pitch axis velocity (pvel). The result is slowed down by controlling the linear slew rate, and this is mixed with the original input to obtain the corrected pitch number as output.
Below that is a graphical representation of the lately linearized note span. Setting the knob to 1/4 results in the left-most graph: here the center 1/4 of the note is fully corrected, and this has the side effect (literally!) of increasing the pitch slope in the 3/4 wide transition regions between adjacent notes. Similarly, setting the knob to 1/2 gives 1/2 note width of correction, 3/4 gives 3/4 correction, and the knob set to full gives us full correction, or steppy quantization, where the notes "pop" from one to the next. Keep in mind that these graphs are showing you what it takes to correct the pitch, not the final corrected pitch.
A main point that gets lost in these technical descriptions: once you've simply slowed the correction down - by slew limiting, or by 1st or higher order low pass filter, etc. - you could actually just stop there as you've accomplished 90% of what we think of as "full" pitch correction, with the remaining features nice to have but not entirely essential - and they can be quite fiddly to implement (look at me, I'm years into this). You don't even need a variable span function because even a little delay will slant the steep edges of steppy quantization, rendering them inaudible. You do need the action of the corr knob though, as this "humanizes" the perfect correction by letting some pitch error back in. Perfect pitch correction is audible with male voice presets, as the rich harmonics interacting with the resonance peaks give the ear a lot of relative pitch cues - remove all pitch variation and it sounds like a car horn. Indeed, many vocal simulators introduce a small random pitch variation to combat this.
For the longest time I thought higher order filters were the way to go here as they impart polynomial-like curves to the transitions. But, just as the shortest distance between two points is a line, linear slewing is the quickest way to transition from off-pitch to on-pitch, and the ear isn't all that sensitive to the shape of the correction. Slowing is actually easier to implement via low pass filter because it functions ratiometrically, so the rate of change is simply set by the cutoff frequency; whereas slew factor is directly proportional to accumulator width, therefore absolute slew rate can be affected by where you place attenuation in the signal path, and in that sense linear slew rate limiting is ironically non-linear. Who would think that exponential decay would be linear? I digress...
Here's the design as of today:
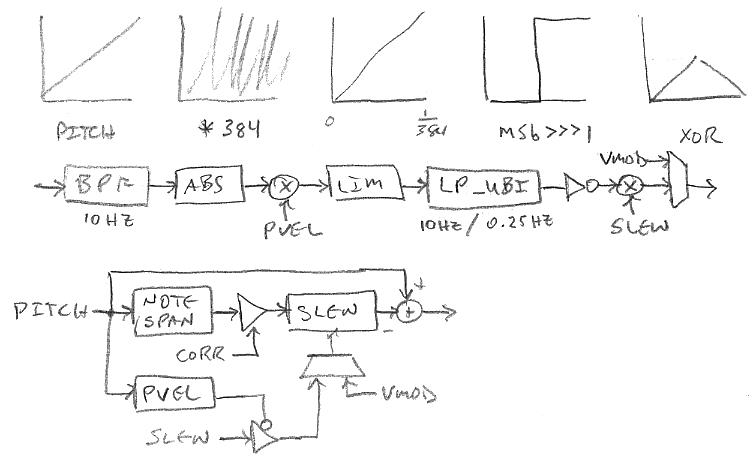
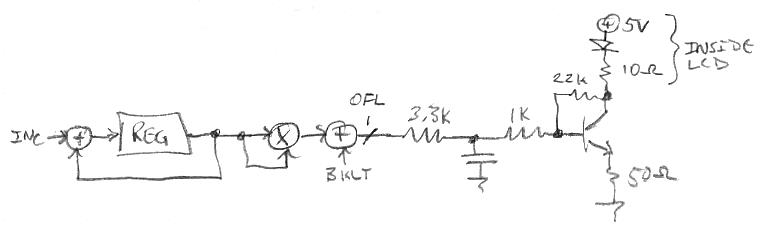
At bottom you can see that the main topological change is that the pitch velocity is now downwardly modulating the slew rate instead of corr, and this rate can be overridden by vmod. I should have drawn the slew|vmod mux in the top diagram as well because it isn't new, though the operation is slightly different. The purpose of the mux is to speed up the slew at very low (generally sub-audible, the location in the volume field can set via the vloc knob) volumes to center up the next note so it comes in on-pitch. The mux comes after any pvel modulation, so it overrides that. I actually tried pretty hard to come up with an arrangement that didn't override pvel, but came up empty. The pvel modulation of slew decreases the slew rate (increases the slew time) when the right hand moves, which helps to mask any steep edges on the correction signal via increased filtering.
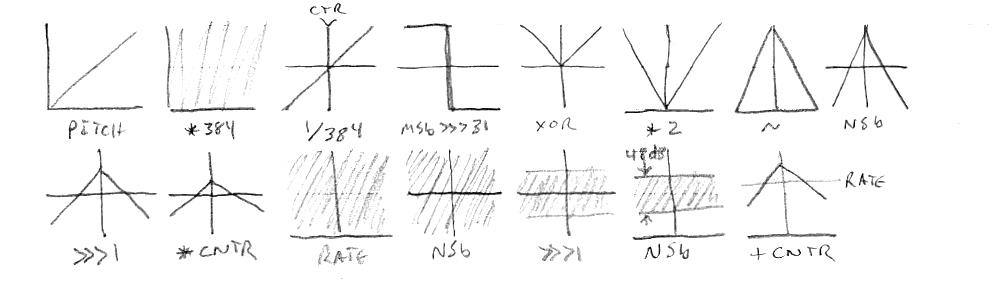
The main problem with conventional velocity detection as applied to pitch correction is that it either has too little gain and doesn't kick in fast / often enough to lower the filter frequency - you hear stepping when span is high, slew is low, and you move your pitch hand too slowly to a neighboring note - or it has too much gain and effectively turns off pitch correction for any pitch hand movement at all. Pvel still has a use though, because it can enable lower slew settings. Seen above is a method I'm using to increase the general usefulness of pvel. Graphically the pitch number is modulo multiplied by the number of notes/octave * octaves (12 * 32) in the linear pitch range, giving us 384 full scale ramps. Looking at a single ramp, we XOR it with its full width sign bit, which gives us a half height triangle for each note. This large scale ramping gains up the velocity detector to movement, and the cyclic nature and low harmonic content give it something significant to "chew on". Just moving the pitch hand from note to note will create signifcant change, and sweeping it through the field will generate a low frequency, high amplitude signal. Anyway, this is fed to the velocity detector shown below the graphs. A bandpass filter removes DC & noise, and gains down all but low frequency changes. Then the absolute value is taken, and this is multiplied by pvel and limited to give a large saturation zone. This is fed to a first order bi-modal low pass filter, which has a cutoff frequency of 10Hz for inputs larger than the output, and 0.25Hz otherwise, creating a kind of doubly leaky peak hold which reacts quickly. Finally a bit inverse changes the direction, and this is used to modulate slew.
I like to include a "berserker" setting to any controls whenever possible. Maximum span gives a very edgy and snappy quantization, minimum none; maximum corr gives 100% correction, minimum none; maximum pvel effectively turns off correction for all but the tiniest of pitch hand movements, minimum off; maximum slew gives over 5 seconds of slew time, minimum 21 ms; and vloc positions vmod over a -96dB to 0dB range. Crazy settings tend to reveal the thing functioning and create audible artifacting. So any real use of this module for unobtrusive pitch correction will necessarily employ the more moderate ranges of at least some of these controls. I tend to use a lot of correction, and my settings are:
slew=16 (1/2)
pvel=16 (1/2)
span=31 (max)
corr=31 (max)
vloc=18 (vmod transition @ -42dB)
Max corr is getting a little fatiguing sounding but I can't bring myself to lower it. Sometimes I up the slew a little for really slow songs, though now I may be able to rely on the improved pvel. One could use even lower slew with higher pvel, but for really low slew some backing off of span is required to reduce low velocity discontinuities, and I think slew should be used as the go-to knob for the overall correcting effect, with the other knobs used as seasoning.