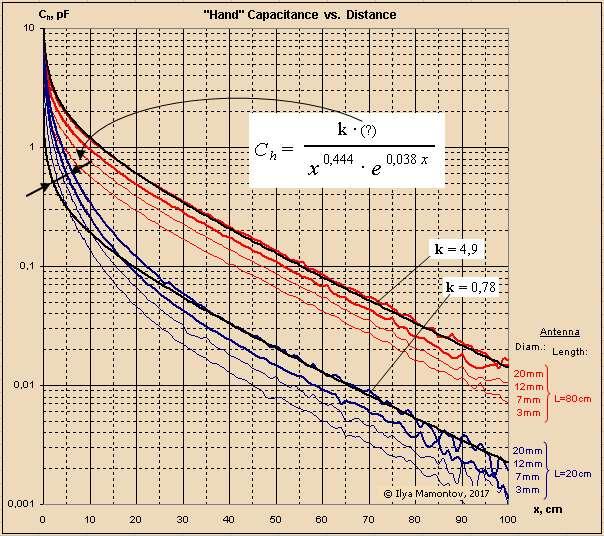
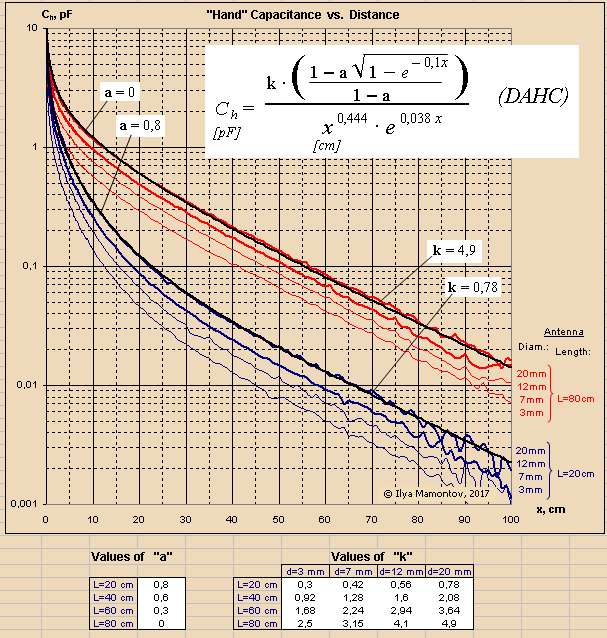
"I watched your interesting dispute with Dewster concerning the 1/d^x (x=1 or 1.7) dependence on hand capacitance in this thread." - JPascal
My various data gathering simulations and experiments led me to believe that C is proportional enough to 1/d for Theremin use, but now I know that isn't entirely true. It's good enough for and entry-level or maybe mid-level instrument, certainly good enough for the volume side, but not good enough for the pitch side of a pro quality Theremin. I'm seeing pretty fantastic linearity with my latest scheme (where I subtract the frequency number from a constant that is slightly larger than it, then take the negative fractional power, and then feed this to an exponential response numerically controlled oscillator to generate the audio tone). I wonder if you have looked into this ILYA?
"It is like a backhand in table tennis in your measurements. The vertical of the area is out of direction to the rod at higher distances. And like a right hand straight punch, in boxing called cross, always perpendicular in Dewsters experimental set. May be the difference is not very high, but is it negligible?"
This is a very good question. Certainly some people play by addressing the antenna with the back of their hand, while others (the majority?) play with their fingers pointing at the antenna. My own data is of a ball/fist. I'm qualifying linearity on my prototype by open/closed hand gestures, which is sort of both I guess. It's very difficult to precisely measure bulk hand movement, but quite easy to make repeatable hand gestures. Having a pitch display is a godsend when doing this BTW.
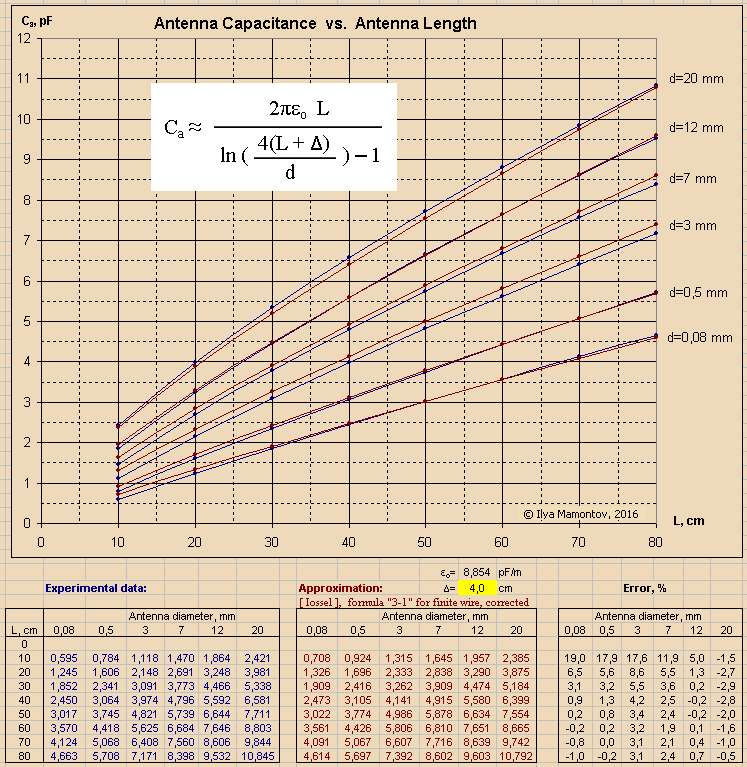
![]() =0.04 m you will achieve the error less 5 % in range L= 30 to 80 cm.
=0.04 m you will achieve the error less 5 % in range L= 30 to 80 cm.