Let's Design and Build a (mostly) Digital Theremin!

"PETG Paintable - no problem, although the paint solvents don't really melt into the PETG, nor is is necessary because of the excellent tooth adhesion where the paint permeates the porosity."  - pitts8r

I'm finding other possible uses for the 3D printed surface texture too.  The pattern formed by the Z layering is quite regular, and so can form the basis of a rather aggressive friction fit between parts with identical Z stepping.  And the same pattern can act as a guide for coil windings, particularly those consisting of finer wire.

It's a Question of Aspect Ratios

I made three single layer air core solenoids, all wound with 1 build insulation 30AWG on PETG 3D printed coil forms, with three different winding aspect ratios (winding length / diameter) of 0.5, 1.0, and 1.88:

The 1.88 aspect ratio coil is the standard kit pitch coil.  For the two larger diameter coils I printed some end caps, which really help to stiffen the otherwise too flexible 4 layer walls.  For larger coils one could also print extra internal stiffeners and perhaps glue them in.  The tallest coil is covered in heatshrink, the other two were instead coated in clear nail polish to secure the windings.

I tested the coils in my test jig, which lowers the drive impedance of the signal generator to approx. 2.4 Ohms, and presents approx. 13.4pF load to the other end of the coil.  Q is directly read as the output / input voltage ratio:

Observations:
- DCR increases with aspect ratio due to the reduction in bulk coupling, which requires more wire to reach the target inductance.
- The self resonance frequency is a measure of the self capacitance of the coil (and its environment).  Lower aspect ratios place the ends of the coil closer together, which increases the self capacitance.
- The 1:1 aspect ratio coil has slightly higher Q than the other coils, but a bit lower self resonance that the 1:1.88 coil.  So 1:1 (or thereabouts) has optimal bulk coupling for resonance with the jig capacitance, but at the expense of an increase in self capacitance.
- Any of these coils would function well in a digital Theremin because the influences of the aspect ratio are broad minima / maxima; ideally one would pick 1:1 or somewhat higher.
- Q is more important than self resonance because it directly increases both the antenna voltage swing and the frequency selectivity. 
- Increased antenna voltage improves external noise rejection.
- Increased frequency selectivity improves both oscillator stability and external noise rejection.

- Q is more important than self resonance because it directly increases both the antenna voltage swing and the frequency selectivity.  - Increased antenna voltage improves external noise rejection.- Increased frequency selectivity improves both oscillator stability and external noise rejection.

Home systems generate broadband signals that are picked up more strongly with a high Q, or so I thought?

"Home systems generate broadband signals that are picked up more strongly with a high Q, or so I thought?"  - JPascal

Q is like a flywheel, with high Q you have to time the interference almost exactly in order to significantly perturb it.  So if the interference has sufficient amplitude and hits the high Q resonance more or less spot-on then yes, it can cause big trouble.  But low Q has a broader resonance, which gives interference a wider "window" to get in.  So we're relying on the interference to be statistically unlikely to hit our high Q system.  Some form of spread spectrum would likely be better in terms of countermeasures here, but that usually means lower Q coils, and thus lower antenna voltages.

I've experimented a bit here: two D-Levs can interfere with each other over several meters, but you have to work at aligning the field frequencies pretty closely (similar antennas and rather slow sweep with the pitch hand) before you notice it.  Absence of evidence isn't evidence of absence, but I haven't had any reports of other Theremins interfering with the D-Lev.  As far as I know (measuring when I have the opportunity, perusing schematics, etc.) the D-Lev has higher voltage fields than most other Theremins.

I understand that the quality factor (Q-factor) of a resonant circuit significantly influences its sensitivity to interference from the environment. If this interference is narrowband and the resonance is far away, a high Q factor certainly has advantages.

My experience e.g. with superhet medium wave radios shows that the interference from the house installation is very strong. With analog theremins, filtering in the RF section is essential to avoid interfering modulation (ugly splitting of the overtones) of the audio signal. 

A digitally processed signal in the D-Lev can be filtered more easily, I suppose.

"...interference from the house installation is very strong."  - JPascal

Do you mean the AC mains electric field?  If so, yes it is quite strong.

"A digitally processed signal in the D-Lev can be filtered more easily, I suppose."

Yes, there are 4 second order notch filters: one at the mains frequency and the rest at the 3 lowest harmonics, plus an 8th order low pass filter that tracks 1 octave below the note being played.

RF Chokes in Series

I was curious as to whether my intuitions regarding RF Chokes in series (like in the Moog Etherwave) held any water.  So I soldered five 50mH Bourns 6310 RF chokes in series and placed on my test jig:

Above: 5 chokes on the test jig, the two on the left are shorted out via the red test lead.

The test jig lowers the drive impedance of the signal generator to approx. 2.4 Ohms, and presents approx. 13.4pF load to the other end of the coils.  Coil count n < 5 was tested by shorting out coils on the drive end with an alligator clip lead.  Small value capacitances were placed in series with the sense end of the jig and coil to test different C loads.  The function generator output voltage was adjusted to be 0.1Vpp at the coil drive end.  Scope BW limiting and averaging were used to enhance measurement of Vpp.

Given (assuming no significant L coupling):
1. Series LCR Q = (1/R) * sqrt(L/C).
2. So if R & L = constant, then Q is proportional to 1/sqrt(C).
3. R and L are proportional to coil count n.
4. So: Q = [1/(n*R)] * sqrt(n*L/C) = sqrt(n)/n * (1/R) * sqrt(L/C) = 1/sqrt(n) * (1/R) * sqrt(L/C)
5. So if R & L & C = constant, then Q is proportional to 1/sqrt(n).

Observations:
- For Jig type capacitive loads, Q is roughly constant over n.  This is unexpected due to (5) above.
- As capacitive load is reduced, Q increasingly favors higher n.
- For free air resonance (FAR) self C is roughly independent of n.

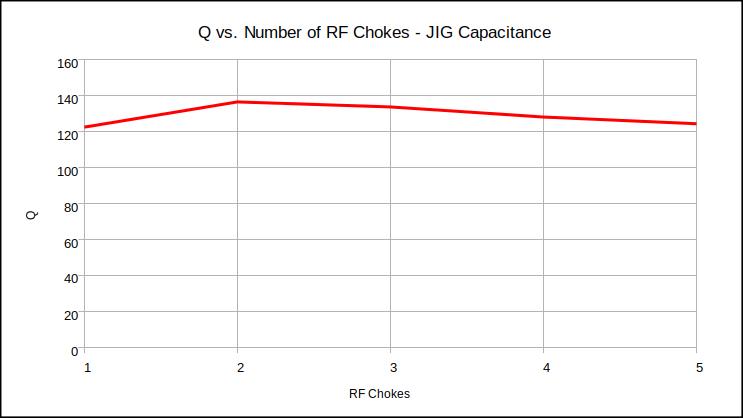
Above: For Jig type capacitive loads, Q is roughly constant over n.

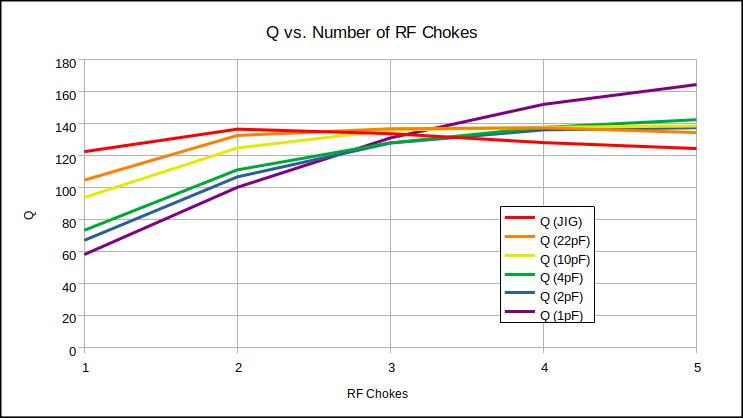
Above: As capacitive load is reduced, Q increasingly favors higher n.  The capacitances here are the series values, not the final load values, which are somewhat smaller.

Above: For free air resonance (FAR) self C is roughly independent of n.