I suspect that this could turn into a controvercial thread, but at the outset, I want to say that its not meant to 'dis' digital - and that I probably dont know what I am talking about in this posting... I just have some ideas and hypotheses I want to share - But most of all I probably have big gaps in my understanding, and I have questions I am sure others here will be able to answer. I am not actually "asking" any "questions" - I am presenting what I think - The "questions" are implied because I am not sure if what I am postulating is valid.
This thread was "inspired" by comments on the open.theremin thread. -
When I say "is" or make any 'declaration' in the following, please understand that this is not a statement of "fact" - I could be wrong about any assertion or calculation I make.. This is NOT my area of competency!
I want to start by ignoring issues such as aliasing etc (although others are welcome to tread this route here) and just look first at the issues which bother me and cause me questions - It may well be that the answers to my questions are embedded in deeper matters which I have not fully understood, and that those answering will need to go into more depth and maths than I would like - but please do - I will try to keep up!
Dynamics:
With a musical instrument employing digital production of the sound (which ends up as a digital word being fed to a Digital to Analogue Converter [DAC]) the output waveforms resolution is defined by two factors:
1:) The number of samples output per second, for example, 48ksps = 48000 samples per second, and
2:) The dynamic level resolution, or how many voltage steps the signal has - for example, 8 bit resolution = 256 steps, 12 bits = 4096, 16 bit = 65535.
My problems / questions are related to the effect on the quality of the waveforms reproduction as dynamics of the signal (amplitude of the waveform) is varied by computation, in order to produce the "envelope", and the resulting loss of resolution for any waveform which is having its amplitude altered by digital computation.
Lets take a sine wave with 12 bit resolution - at full output level one gets a highly respectable 4096 step reconstruction of this wave. If one has a volume controller (envelope generator, volume antenna, whatever) acting on this signal before the D/A (as in, dividing the level of each value being fed to the D/A to exert control of the output) then each 6db drop in volume equates to an effective loss of one bit in that waveforms resolution - so:
-0db (full volume) = 12 bit = 4096 steps; -6db = 11 = 2048; -12db = 10 = 1024; -18db = 9 = 512; -24db = 8 bits = 256 steps...
From the above, it can be seen that as the attenuation applied by the controller function gets to -24db, the resolution of (an originally 12 bit) waveform will have dropped to 8 bits.. My expierience is that (to my ears) 8 bits still gives just about acceptable resolution for signals which are not too complex..
But when a complex waveform goes below about 8 bits, I really start to notice it – I think that what happens is this:
Any components of the waveform which are below the level of the possible resolution of that waveform, are lost – lost, essentially, due to the quantizing, in the noise floor – results which sit between two bits “steps” will be either “assigned” to the lower or the higher step – At best, there is a 1 bit noise ‘jitter’ – so as the waveform is divided by the dynamics operations, the resolution of the lower quantity components are affected more severely – and as (with most waveforms) it is the higher harmonic components which are at lowest amplitude, it is these which get lost most rapidly into the noise floor –
With an 8 bit waveform, one can resolve components perhaps down to -42db, a 6db reduction in this waveform (down to 7 bit) and components below say 36db will be lost.. Oh, there will be a 6db reduction in all components of the waveform – but components which drop below the noise floor are lost – they are gone – And to my ears, an 8 bit waveform subjected to digital (computed) amplitude control sounds as if a noisy low pass filter is being applied as the level is reduced.
Most of what I say here is based on memory of my experiments in the late ‘70s / early ‘80s when I was designing and building synthesisers – Like many at that time, I was exploring digital waveform generation / wavetables etc.. And I was using ancient clunky components I could afford.. 8 bit DAC’s like the DAC0800 were ideal as one could buy compatible 8 bit static RAM and EPROM on 0.1” pitch and build a whole wavetable DCO using a simple 8 bit processor or even using standard logic..
I appreciate that nobody is proposing an 8 bit computed digital musical instrument! ;-)
But it seems to me that the reduction of fidelity must apply regardless of how many bits are employed for the wave table – ok, the difference is that if one starts with a 16 bit waveform, one has an extra 42db’s “headroom” before one gets to 8 bit resolution.. But as the computed level drops, the quality of the waveform is degraded.. The only important issue is whether this degradation becomes audible, or whether it only starts to occur at levels where the sound is inaudible.
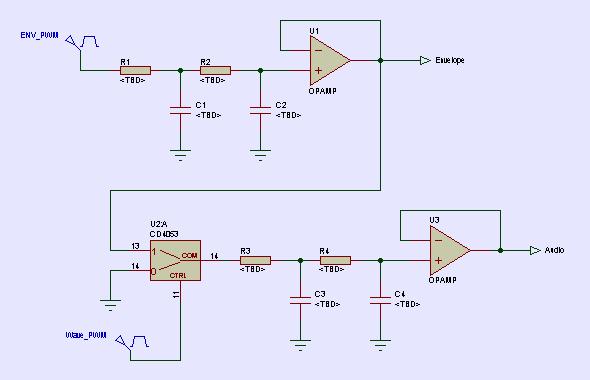
In order to get reasonable fidelity from my synth, I first used mixed signal (mixed analogue and digital) techniques, having an 8 bit MDAC outputting the waveform, and controlling the amplitude from an analogue signal (voltage) – Then used two DAC’s (one as an MDCAC for the waveform, one to control dynamics) – this method results in a waveform which does not degrade as the amplitude is changed.
Looking at the open.theremin, I wonder if using two 12 bit DAC’s in a similar manner might not give far better sound quality than increasing the digital resolution to say 16 bits could.
A small diagram here shows the idea.
Fred.