Vadim, I believe that my "oscilloscope axis processing" approach [link] is extremely similar to the approach you've investigated here lately, though mine is a first order integrate-and-dump process, and yours is a more continuous second order process. Mine uses the measurement period to kill hum, and I'm wondering if yours could be adapted to do the same? Could you somehow arrange things so that the "ends" of the difference are 1/60Hz or 1/50Hz apart? Or close to this? The first order process really kills hum (you can clearly see this on the scope by setting the horizontal delay to something substantially different than the inverse of the mains frequency) but allows RF to alias. Your second order process could kill hum and some RF too.
Main Hum Noise investigations.
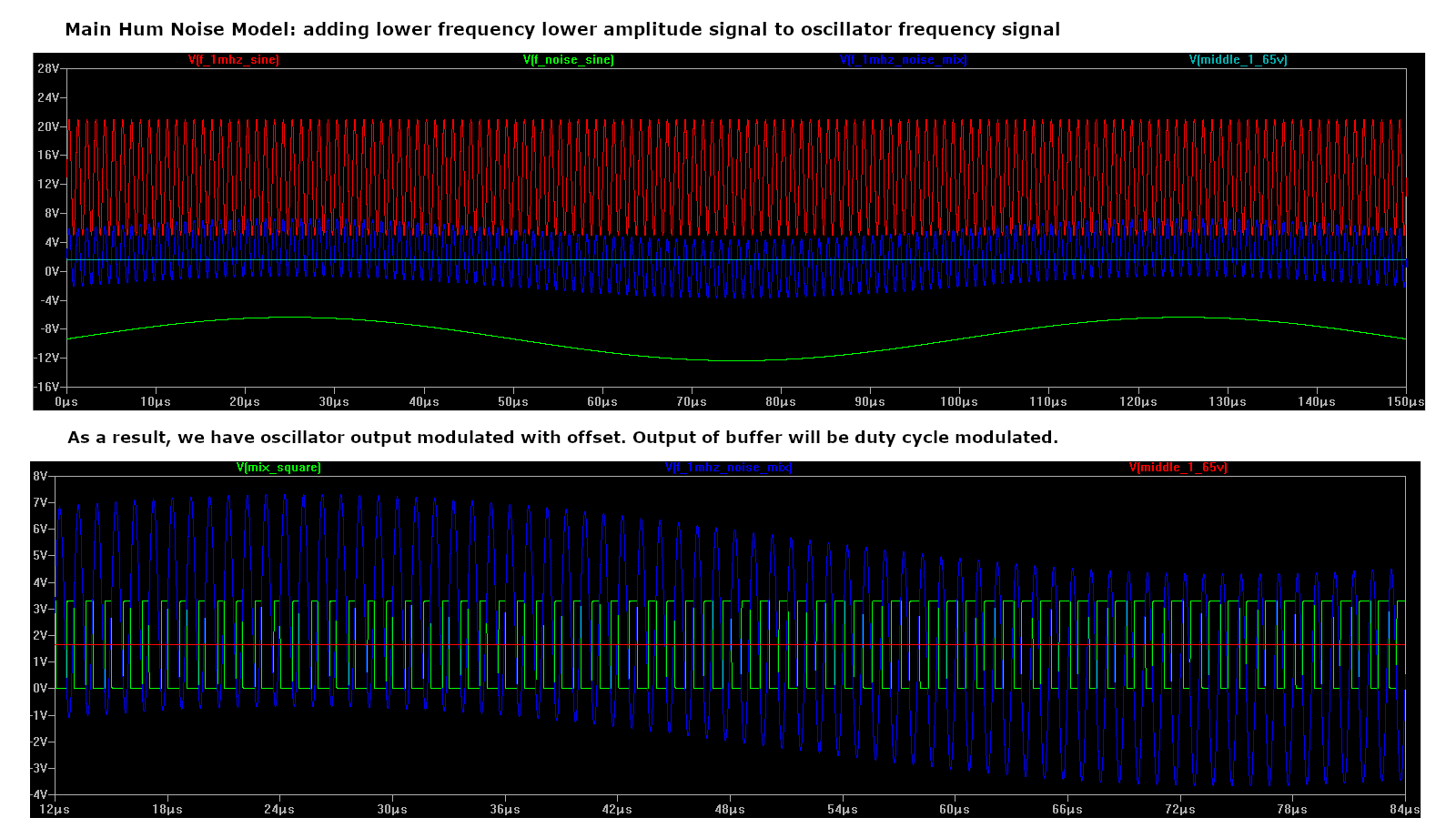
Trying to understand how main hum noise is visible in oscillator square output.
Assuming that 50 or 60 Hz periodic, almost sine, signal is added to oscillator signal.
It has 15000..20000 lower frequency and much lower amplitude than main oscillator signal.
I believe it works like slowly changing "DC Offset" for oscillator output, resulting in PWM duty cycle modulation of oscillator output.
On simulation results below, higher amplitude and higher frequency noise signal is used to emphasize effect introduced by noise to oscilaltor square output.
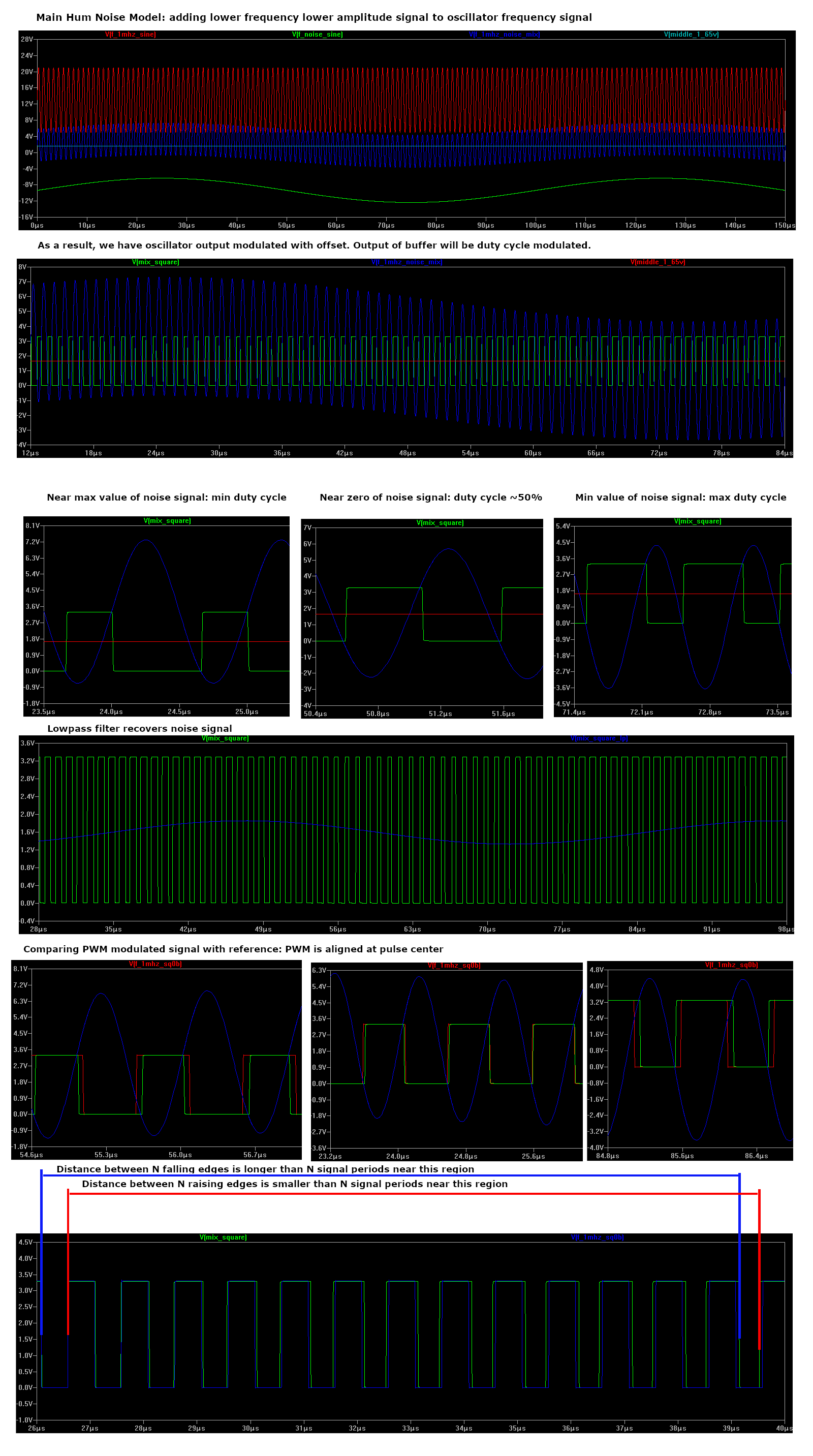
On last image we can see that if we try to calculate oscillator signal period based on raising or falling edges, we will have different values at different points, depending on local main hum noise offset.
At points near noise crossing zero, difference is almost 0. But near noise peaks, we can see maximum error values introduced by noise.
Error value (difference between measured signal period and real exact value) will be 50 or 60Hz sine with some amplitude. For far hand distance this offset will produce audible modulation of calculated hand to antenna distance.
How can we suppress it? Bandstop filter at noise frequency? No! There is a simple solution.
Oscillator output signal has duty cycle modulated by lower frequency (main hum). But fortunately, pulses are actually (almost) synchronous to pulse center points.
If we take pulse centers (average between raising and falling edge, or falling and raising) we will get positions of oscillator signal peaks instead of zero crossing.
Peak positions are not affected by DC offset, and can be used for calculation of oscillator signal period with noise removed.
The only concern: near noise peak, middle point between raising and falling edge is accurately centered at oscillator signal peak. But between peaks (with max effect near noise zero crossing),
"DC offset" from horizontal line is transformed to raising and falling, giving offset of middle edge position from real peak value. But I hope this effect is eliminated by high F_osc/F_noise rate.
"DC offset" inclination is stretched 15000 times, producing "almost const" at oscillator period scale. As well, it's reduced by high V_antenna / V_noise rate.
Initial plan of Teensy 4 sensor was:
Oscillator square output passed to 240MHz time capture input: timer will capture timer counter values at raising and falling edges of input signal and write them to circular buffer using DMA.
Captured values have low precision: for 1MHz oscillator frequency, timer counter changes ~240 times per one oscillator period.
Difference between edge position and position of previous edge of same type will be only ~280 == ~8 bits. But since signal period changes only by 5% for whole working hand to antenna distance, only 3.5 bits of 8 provide hand position information.
We can use averaging to collect more bits.
Taking position of both edges gives 1 more bit.
Stage 1 processing: subtract recent edge position from same edge position delayed by N oscillator cycles - gives log2(N) exact bits, introducing N/2 oscillator periods latency (averaging signal for N periods).
Stage 2: 4 stage IIR on stage 1 output to extract more useful bits from lower bits dithering of stage 1 output.
Simulation shows that for 99% of oscillator frequencies it's possible to collect >=28 bits of meaningful bits.
Although, the rest, near rational multiply points F_timer * A / B, there are artifacts which reduce number of bits to 20-22. Anyway, it should be enough for distances up to 60cm.
Let's modify averaging algorithm to filter out main hum noise.
Actually, it's already filtered out (it's a reason why I was unable to reproduce it on simulation).
From stage 1, samples are coming interleaved, corresponding to falling / raising edges. Average of two sequential values is actually exact oscillator frequency period. Stage 2 filter filters out odd/even samples jumping.
But just in case, we can modify stage 1.
Instead of returning (sample_buffer[pos] - sample_buffer[pos - N]), we can return (sample_buffer[pos] + sample_buffer[pos-1] - sample_buffer[pos - N] - sample_buffer[pos - N - 1]) which gives difference between peaks instead of edges.
FPGA implementation
While waiting for my small oscillator PCBs for Tube Monster design (they are leaving chinese customs now), I've reimplemented Xilinx FPGA based sensor with new design.
While designing, I'm trying to minimize resource usage still keeping high sensitivity.
Stage 0: oversampling_edge_detector module - provides sequence of timer counter values captured on each input pin edge. Low frequency timer counter is working at 150MHz. Worse than Teensy 4? No.
There are ISERDESE2 modules implementing 600MHz*DDR=1200MHz signal deserialized 8-bit values at 150MHz. Optionally 2 / 4 / 8 of such modules can work together to provide 16, 32, or 64 deserialized bits per 150MHz cycle.
IDELAYE2 modules are used to provide different input delay for each of ISERDESE2. Delays are distributed equally to cover 1200MHz period.
With x8 delay based oversampling, module measures edge position with 9.6GHz cycle precision.
Lower 3..6 bits of module output are gained using oversampling, higher bits are low frequency counter bits.
Code:
module oversampling_edge_detector
#(
// oversampling bits, 0=no delay based oversampling, 1=combine 2 iserdes, 2=combine 4 iserdes, 3=combine 8 iserdes
parameter OVERSAMPLING = 3,
// reference frequency for delay line, in MHz
parameter DELAY_REFCLOCK_FREQUENCY=200.0,
// number of bits in timer cycle counter (8 bits for 150MHz->1MHz, 6 bits for max filter stage1 delay)
parameter COUNTER_BITS = 8 + 6
)
(
// ~600MHz
input logic CLK_SHIFT,
// ~600MHz, phase inverted CLK_SHIFT
input logic CLK_SHIFTB,
// ~150MHz, must be phase aligned CLK_SHIFT/4
input logic CLK,
// reset, active 1, must be synchronous to CLK_SHIFT !!!
input logic RESET,
// counter enable, active 1, keep inactive for 4 CLK_SHIFT cycles adter RESET deassertion
// must be synchronous to CLK_SHIFT !!!
input logic CE,
// serial input
input logic IN,
// 1 for one cycle if state is changed
output logic CHANGE_FLAG,
// 1 if change is raising edge, 0 if falling edge
output logic CHANGE_EDGE,
// counter value for edge
output logic[3 + OVERSAMPLING + COUNTER_BITS - 1 : 0] EDGE_POSITION
);
Resource utilization for max oversampling (9.6GHz resolution, 14 bits output), recommended for Pitch axis:
+-----------------------------+------+-------+-----------+-------+
| Site Type | Used | Fixed | Available | Util% |
+-----------------------------+------+-------+-----------+-------+
| Slice LUTs* | 56 | 0 | 17600 | 0.32 |
| LUT as Logic | 56 | 0 | 17600 | 0.32 |
| LUT as Memory | 0 | 0 | 6000 | 0.00 |
| Slice Registers | 86 | 0 | 35200 | 0.24 |
| Register as Flip Flop | 86 | 0 | 35200 | 0.24 |
| Register as Latch | 0 | 0 | 35200 | 0.00 |
| IDELAYE2/IDELAYE2_FINEDELAY | 8 | 0 | 100 | 8.00 |
| IDELAYE2 only | 8 | 0 | | |
| ILOGIC | 8 | 0 | 100 | 8.00 |
| ISERDES | 8 | | | |
+-----------------------------+------+-------+-----------+-------+
Resource utilization for min oversampling (1.2GHz resolution, 11 bits output), recommended for Volume axis:
+-----------------------------+------+-------+-----------+-------+
| Site Type | Used | Fixed | Available | Util% |
+-----------------------------+------+-------+-----------+-------+
| Slice LUTs* | 12 | 0 | 17600 | 0.07 |
| LUT as Logic | 12 | 0 | 17600 | 0.07 |
| LUT as Memory | 0 | 0 | 6000 | 0.00 |
| Slice Registers | 20 | 0 | 35200 | 0.06 |
| Register as Flip Flop | 20 | 0 | 35200 | 0.06 |
| Register as Latch | 0 | 0 | 35200 | 0.00 |
| IDELAYE2/IDELAYE2_FINEDELAY | 0 | 0 | 100 | 0.00 |
| ILOGIC | 1 | 0 | 100 | 1.00 |
| ISERDES | 1 | | | |
+-----------------------------+------+-------+-----------+-------+
Stage 1: delay_diff_filter module - takes output of stage 0 (sequence of timer counter values, interleaved captured on raising / falling / ... edges).
On each new input value, we put it to circular delay buffer and calculate new output value.
OUT = BUF[pos] - BUF[pos - DELAY_CYCLES]
This stage gives additional exact log2(DELAY_CYCLES) useful bits of data, introducing (1/F_osc)*DELAY_CYCLES/4 latency.
Code:
module delay_diff_filter
#(
// filter will calculate diff with value delayed by DELAY_CYCLES WR cycles, power of two is recommended
parameter DELAY_CYCLES = 64,
// number of bits in value (the bigger is delay, the more bits in value is needed: one addr bit == +1 value bit)
parameter VALUE_BITS = 20,
// use BRAM for delays with log2(DELAY_CYCLE) >= BRAM_ADDR_BITS_THRESHOLD
parameter BRAM_ADDR_BITS_THRESHOLD = 7
)
(
// clock signal, inputs and outputs are being changed on raising edge of this clock
input logic CLK,
// reset, active 1
input logic RESET,
// input value for filter
input logic [VALUE_BITS - 1 : 0] IN_VALUE,
// set to 1 for one clock cycle to push new value
input logic WR,
// filter output (IN_VALUE - delay(IN_VALUE, 2**DELAY_ADDR_BITS)), updated one cycle after WR
// delay is counted as number of input values (WR==1 count)
output logic [VALUE_BITS - 1 : 0] OUT_DIFF
);
Resource utilization for 64 cycle delay (32 F_osc cycles averaging period, 16 F_osc cycles latency introduced), based on distributed RAM:
+----------------------------+------+-------+-----------+-------+
| Site Type | Used | Fixed | Available | Util% |
+----------------------------+------+-------+-----------+-------+
| Slice LUTs* | 47 | 0 | 17600 | 0.27 |
| LUT as Logic | 27 | 0 | 17600 | 0.15 |
| LUT as Memory | 20 | 0 | 6000 | 0.33 |
| LUT as Distributed RAM | 20 | 0 | | |
| LUT as Shift Register | 0 | 0 | | |
| Slice Registers | 27 | 0 | 35200 | 0.08 |
| Register as Flip Flop | 27 | 0 | 35200 | 0.08 |
| Register as Latch | 0 | 0 | 35200 | 0.00 |
| F7 Muxes | 0 | 0 | 8800 | 0.00 |
| F8 Muxes | 0 | 0 | 4400 | 0.00 |
+----------------------------+------+-------+-----------+-------+
Resource utilization for 512 cycle delay (256 F_osc cycles averaging period, 128 F_osc cycles latency introduced), based on distributed RAM:
+-------------------------+------+-------+-----------+-------+
| Site Type | Used | Fixed | Available | Util% |
+-------------------------+------+-------+-----------+-------+
| Slice LUTs* | 34 | 0 | 17600 | 0.19 |
| LUT as Logic | 34 | 0 | 17600 | 0.19 |
| LUT as Memory | 0 | 0 | 6000 | 0.00 |
| Slice Registers | 30 | 0 | 35200 | 0.09 |
| Register as Flip Flop | 30 | 0 | 35200 | 0.09 |
| Register as Latch | 0 | 0 | 35200 | 0.00 |
| F7 Muxes | 0 | 0 | 8800 | 0.00 |
| F8 Muxes | 0 | 0 | 4400 | 0.00 |
| Block RAM Tile | 0.5 | 0 | 60 | 0.83 |
| RAMB36/FIFO* | 0 | 0 | 60 | 0.00 |
| RAMB18 | 1 | 0 | 120 | 0.83 |
| RAMB18E1 only | 1 | | | |
+-------------------------+------+-------+-----------+-------+
stage2: iir_nstage_pow2k module - IIR filter with 1..8 stages and K = (1 / power_of_two) (using simple shift). Number of stages and shift bits are configurable at compile time.
Updates value once per CYCLE_COUNT clock cycles. CLK/CYCLE_COUNT should be multiple of audio sample rate (48000) to avoid aliasing. Although 150MHz is multiple of 48000, it's strange multiple. It's 5**5.
Instead, it makes sense to use clock domain converter, and select more suitable multiple of 48000 as IIR filter clock.
Number of cycles and number of IIR filter stages is configurable independently - to allow synchronization between IIR output update rate and audio sample rate.
This stage smoothes input data providing more useful bits from averaging.
Recommended value bits: 30-36.
To minimize resource utilization, single pair of subtractor+adder is reused for all stages. Register bank is used to store state for each stage.
It allows to increase number of stages (up to 32) w/o increasing of resource usage. The only cost is increased number of CLK cycles per one output value.
Code:
module iir_nstage_pow2k
#(
// filter coefficient is 1 / (1 << K_SHIFT_BITS) : instead of multiply, right shift is used
parameter K_SHIFT_BITS = 6,
// number of bits in filter input and output
parameter VALUE_BITS = 30,
// filter output is being updated once per CYCLE_COUNT (can be bigger than number of stages to align output rate with other clock)
parameter CYCLE_COUNT = 5,
// number of IIR filter stages, should be <= CYCLE_COUNT
parameter STAGE_COUNT = 5
)
(
// clock signal, inputs and outputs are being changed on raising edge of this clock
input logic CLK,
// reset, active 1
input logic RESET,
// filter input value
input logic [VALUE_BITS-1 : 0] IN_VALUE,
// filter output value
output logic [VALUE_BITS-1 : 0] OUT_VALUE
);
Resource utilization for 5 stages, 6 shift bits K, 30 bits for value:
+----------------------------+------+-------+-----------+-------+
| Site Type | Used | Fixed | Available | Util% |
+----------------------------+------+-------+-----------+-------+
| Slice LUTs* | 95 | 0 | 17600 | 0.54 |
| LUT as Logic | 75 | 0 | 17600 | 0.43 |
| LUT as Memory | 20 | 0 | 6000 | 0.33 |
| LUT as Distributed RAM | 20 | 0 | | |
| LUT as Shift Register | 0 | 0 | | |
| Slice Registers | 67 | 0 | 35200 | 0.19 |
| Register as Flip Flop | 67 | 0 | 35200 | 0.19 |
| Register as Latch | 0 | 0 | 35200 | 0.00 |
| F7 Muxes | 0 | 0 | 8800 | 0.00 |
| F8 Muxes | 0 | 0 | 4400 | 0.00 |
+----------------------------+------+-------+-----------+-------+
Resource utilization for 5 stages, 6 shift bits K, 36 bits for value:
+----------------------------+------+-------+-----------+-------+
| Site Type | Used | Fixed | Available | Util% |
+----------------------------+------+-------+-----------+-------+
| Slice LUTs* | 111 | 0 | 17600 | 0.63 |
| LUT as Logic | 87 | 0 | 17600 | 0.49 |
| LUT as Memory | 24 | 0 | 6000 | 0.40 |
| LUT as Distributed RAM | 24 | 0 | | |
| LUT as Shift Register | 0 | 0 | | |
| Slice Registers | 79 | 0 | 35200 | 0.22 |
| Register as Flip Flop | 79 | 0 | 35200 | 0.22 |
| Register as Latch | 0 | 0 | 35200 | 0.00 |
| F7 Muxes | 0 | 0 | 8800 | 0.00 |
| F8 Muxes | 0 | 0 | 4400 | 0.00 |
+----------------------------+------+-------+-----------+-------+
Top resource usage for all 3 stages: 56+47+111 = 214 LUTs.
For Volume axis, lower precision implementation with lower resources may be used.
Expected number of meaningful bits is 26-32.
Sources can be found on github