"moreover, one of multiplications can be excluded if the amplitude symmetry between sine and сos is not required." - ILYA
True, but then the sine frequency would be related to square root of the multiplier input, which is kind of awkward.
I (perhaps too) quickly sketched out what this would look like in digital logic:

This is basically an infinite Q state variable filter that is initially stimulated and allowed to ring forever. Quite surprisingly, round off errors don't cause it to gain or lose energy over time. The blocks "SIN", "COS", "FREQ", and "AMPL" are dual port BRAMs. Not shown here (for clarity) is the additional registering between multiplies, adds, etc. to pipeline and speed things up, nor is address generation shown. It would take three 18x18 multipliers and 16k words (18 bits wide) of BRAM. Given a top speed of 200MHz for the multipliers, it could generate over 4000 sine waves of arbitrary frequency and amplitude at the sampling rate of 48kHz. Though changing the frequency on the fly might alter the amplitudes.
A more direct method is this:
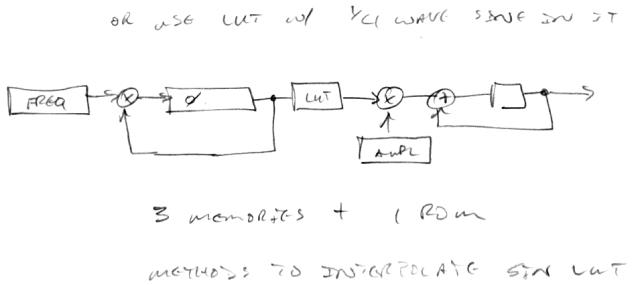
Here a phase accumulator indexes a sine wave ROM. The blocks "FREQ", "PHASE", and "AMPL" are dual port BRAMs; "LUT" is the single port ROM. There are ways to drastically reduce the size of the ROM (store 1/4 wave, linear and higher polynomial interpolation, frequency / phase dither, etc.). It uses two less multipliers, and one less BRAM but that is taken up by a potentially larger ROM. It is basically stable because there is no ringing or feedback going on, just phase accumulation. It could supply the same ~4k sine waves as the previous circuit.
[EDIT] Oops, I screwed up on the input to the phase accumulator in the second method. It should sum both the current phase value and some input value, so a multiplier isn't needed there (but one is still required for the amplitude section following).
In the first method I also left out a mux going to the sine input, similar to the one on the cos input, but with a fixed input of zero.
If I were to pick between these methods I'd probably go with the second.

