Let's Design and Build a (mostly) Digital Theremin!

I haven't tried this but you might try adding some +/- noise to the NCO increment too.  

What are you doing about dynamics?  With a fixed glottal waveform, louder and softer sounds like someone adjusting a volume control.  Not realistic at all.

quotation: "A tunable active filter with three quasi-resonant frequency points.

.... Such a filter is the basis of formant speech synthesizers.

In them from the harmonic rich signal there are three frequency bands (formants),

 which after addition in the summing device give a vowel sound. "

https://image.ibb.co/gF1G2G/p0067.jpg

(the end of the article is - https://image.ibb.co/hdU8Gb/p0068.png)

-------------------------------------

But this is not applicable to the theremin, because it does not have "rich in harmonics (overtones) signal."

Checked personally :-)

The difficulty in enriching the sinusoid (yes at least a rectangle!) With a lot of harmonics and overtones.

"The difficulty in enriching the mean and poor sinusoid (yes at least a straight man!) With a lot of harmonics and overtones."  - Martel

Yes, and not just any harmonics and overtones, but certain ones, and with variation based on the volume hand.  When I lower the squaring of my sine wave mutator there are fewer harmonics (it sounds like a low pass filter is getting stronger).  When I switch the mutator to all quadrants producing a rounded square wave, the result doesn't sound very human.

=========

Found a very nice summary PhD thesis: "HMM-based Speech Synthesis Using an Acoustic Glottal Source Model" by Joao Paulo Serrasqueiro Robalo Cabral (link).  I don't care (at this point) about articulating the vocal sounds but it's got plenty of background and references.

"I haven't tried this but you might try adding some +/- noise to the NCO increment too.   What are you doing about dynamics?  With a fixed glottal waveform, louder and softer sounds like someone adjusting a volume control.  Not realistic at all."

About dynamics, well, I have a typical envelope generator from my synth project, not sure yet whether its linear or exp attack is perfectly adequate, but it sounds ok, I can even assemble a few intelligible words by stringing together a few vowels + consonants with envelopes for each, just need to implement morphing between them to get e.g. better diphtongs.

Btw, interesting link in the later post! (joao thesis)

I think ADSR type envelopes might mask issues with ultra slow attacks as are capable on the Theremin?  Cool that you can do articulated speech.

After spending all day in a spreadsheet sim (analyzing a ringing 2nd order filter with negative and positive damping phases idea that didn't pan out) I'm back to looking at artificial (i.e. mathematical) generation of the glottal pulse.  There is an old 1970 paper by Rosenberg ("Effect of Glottal Pulse Shape on the Quality of Natual Vowels") which does human listener A/B testing using various glottal pulse shapes, and a third order polynomial (3rd order rising, 2nd order falling) wins.  A more recent paper ("A New Approach to Parametric Modeling of Glottal Flow" Tahir Mushtaq & Khalid Saifullah, 2011) uses what looks like 3rd order all around (the falling edge "blends" rather than just slams into the x axis) but is actually based on a mass & spring model.  With any experience at all generating naive audio waveforms in DSP, one can see aliasing coming a mile away, so I'm partial to no sharp edges and the more rounding the better, though I realize the harmonics have to come from somewhere.  Beyond rounding, the trick is probably to keep the rate of the edge that generates them below some maximum value.  Once there are sufficient harmonics it seems the smoothness of the spectra is also an issue, as any lumpiness can negatively interact with the formant amplitudes.

I just looked at the spectra of my "poor man's" glottal function.  When set to 4 squarings I see a pretty even row of harmonics that smoothly roll-off of 24dB per decade, though the harmonic 2 and 9 are a slightly lower than the others.  With 3 squarings there's about 28dB per decade.  Some papers talk about 12dB per octave, which is 40dB per decade, and I get this with 2 squarings and very little aliasing.  I think I'm probably overdoing it in the glottal harmonics department, less actually sounds better to me now.

What I don't get at all is some researchers seem to use what looks like the glottal pressure wave (~chopped tops of slanted cosines) directly with good results, and other use the derivative (a + bump with a - sharp tooth).  They seem to be two entirely different animals.  Perhaps the derivative version is for the normalized skewed up formants that some methods are partial to?

Glottal wave:
Yeah, paper's I've seen all describe how to mathematically produce the movement / air flow of vocal folds, which doesn't translate to a bandlimited waveform (unless you dream in math I guess).
I wonder, could one generate a glottal wave cycle by such methods, sample that into a buffer, look at the spectrum which will have aliases, and if you cleverly pick the fundamental of that waveform with respect to the samplerate, mirrored-back aliases would not coincide with harmonics, so you could run some code over the FFT bins and remove peaks which are not multiples of your fundamental, and then you have a "cleaned up" spectrum that you can use to generate a wave table again?

I feel so dirty. I just found a site with depictions of glottal waveforms without vocal tract.
But didn't see some handy CSV file or so for download.
So I copied the image, removed anything not-curve, had my gfx program of choice interpolate the material to a higher resolution / smoothe things a bit, convert to 1bit, then let some code run over it to extract a 1D table of samples from that.
Yes, there is alias in there :-D But not to a horrible extent. That table now actually works, I can get an intelligible female voice now using female f0 pitch and formants - that didn't work too well with the sawtooth, which I will keep, though, for when I actually want a robot voice ;-)

I get the math angle in the papers, they're desperate for a stable model they can feed parameters to and have it give known, repeatable behavior, particularly when it's just a part of a bigger articulated research system.  I'm more interested in organic behavior.  I need it to track pitch accurately, but that's about it.

I'm learning to recalibrate my ear to vocal overtone levels, and can tell now that a sawtooth has way too much harmonic content.  Which is great because it sprays aliasing all over the place.

That Electroglottography site you point to is interesting. It's makes sense but it's confusing to reconcile with how the academic papers describe what's going on at various points of the waveform:

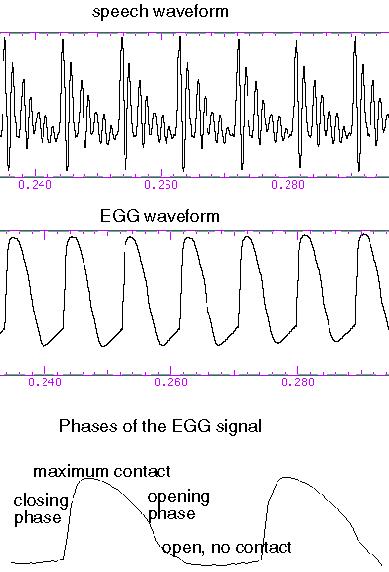
Above, the flat section is labeled as where the glottis is open rather than closed.  And the abrupt closing part is rising rather than falling.  I suppose reversing things in time gives identical spectra?

It does look very similar to my "poor-man's" glottal wave set to 2 squarings:

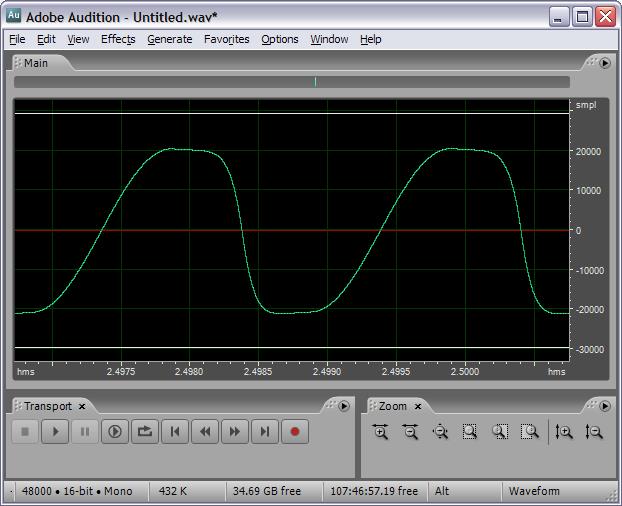
The smooth rise from negative to positive is just the unadulterated sine.  The flattened top, sharp fall, and flattened bottom are from the flipping and repeated squaring of the two center quadrants.  So you get a nice tilted deal with a fast edge, a slow edge, and rounding everywhere. And the integer computations to get it are exceedingly trivial.  Here's the spectra:

I think it's best to not generate any unneeded harmonics in the first place, as removing their alias products later is generally a can of worms.  

==========

Ideally, I'd like my vocal synthesis to be able to go from a non-tonal breath / whisper to fully tonal singing voice, based on the left antenna value. It's pretty easy to get a band-pass state-variable filter to oscillate with a noise input, and dynamically altering the Q doesn't seem to inject much noise into the process.  So I'm going to try feeding a band-pass SV with variable amplitude noise, modulate the Q based on dynamics, and feed the result to some sort of mild distortion function, followed by the formant filter bank.

[EDIT] Played with that a bit and using band-pass filtered noise directly doesn't seem to be a good approach because the amplitude of the resonance bobbles around (which makes sense).  What's mainly causing the oscillation in the vocal tract is air pressure from the lungs vibrating the vocal chords.

Glottal Wave Shaping via Bi-Damped SV Filter

Playing with a dynamically damped SV (state variable) filter in Excel. The basic setup is just feeding a sine wave to a single second order filter. If you design the filter so that both integrators have damping feedback, and then modulate that damping within the cycle you can get very academic "glottaly looking" waveshapes:

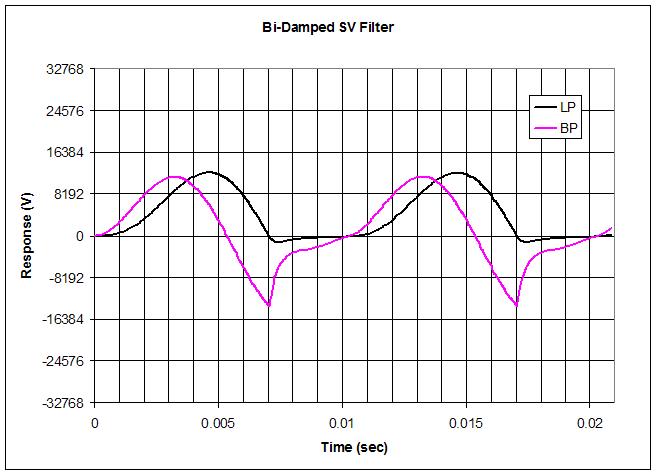
Above shows the bandpass and lowpass integrator outputs.  The damping modulation is simply switching from one fixed damping value to a second larger fixed damping value when the lowpass signal goes negative.  Above the damping values are 0.5 and 5.  The open and closed times can be varied by altering the ratio of the filter center frequency to the input sine frequency, above the ratio is 1.  Haven't actually tried this in hardware yet, but in simulation it all seems to track without being super-fiddly (unlike all the non-linear iterative backwards math in the papers).  The spreadsheet is here if you want to play along at home (my "poor-man's" glottal mutation sim is on the second worksheet page).

Interesting method!
As for sawtooth, it seems the harmonic richness can serve its purpose when tamed somewhat.

Audio file (may be loud)

(some stereo reverb added in Audacity for fitting aural context. And randomly fiddled with the pitch)
The high end of the source wave is rolled off starting at ~ 2kHz with 12dB/oct, played in mezzo/soprano range with a +/- 100cent vibrato, using female formants.
Not Birgit Nilsson, but it produces some nice tones, or tones which show potential of what I might be able to do with this stuff that I wasn't thinking of before playing around with it, but isn't that always so ;-)

EDIT:
Now I, the dillettante layman, tries to explain to himself how this "We have an opera voice now??" accident happened.
The female formant setup I used model a normal "speech mode" vocal tract. They do not model a changed vocal tract due to the lowered larynx of the operatic voice. The larynx position is one thing done different from "regular vocalization", another is tighter cords and more wind pressure to compensate that (I think). Does this produce more overtones, like my sawtooth, some of which I then darken with that 2kHz LPF (longer vocal tract -> darkening?)?
In other words, does the sawtooth + LPF combo imitate the low larynx with tighter cords, then feeding into the upper throat/mouth area which are still modeled by the regular female formants? (I don't know about the raised soft palate, from the sound, it doesn't appear to be missing, but it shouldn't be in the speech formants, I guess, perhaps the sawtooth also helps with that)

Very nice tinkeringdude!  What are you rendering this in (what's your synth)?  And I approve of ogg files (most of my music collection is ripped to ogg).

I would think a lowered larynx might lower at least one of the formants?  The three "pipes" in the 'Y' come together and the lowest branch is getting lengthened.  For some reason it's weird to feel this lowering consciously with my fingers on my throat.

I think it was the Rosenberg paper that stated something like "the glottal source has zeros but the the vocal tract consists only of poles".   He also states that rolloff of speech and the glottal source is somewhere around 12dB per octave.  At any rate, the goal seems to be to get the resonance coloration as independent of the glottal source as possible (at least for research purposes).  In practical terms, this probably means that vowels should sound largely the same regardless of pitch.

[EDIT] Actually, what you're doing (sawtooth + LPF) makes a lot of sense as it gives you a nice even spectra that you can adjust the tilt to.  That seems to be the goal of a lot of the glottal pulse shaping.  In the more complex glottal waveforms the rate of the return to zero is discussed as effectively LPF.