Dominik, I'm studying your excellent video closely (what camera do you use?) but can't quite tell certain things from it due to the fast timing. If you would be so gracious as to relieve my confusion:
1. It seems there is a diode or similar which favors the attack?
2. It seems there is a fixed RC decay time, could you perhaps tell me what that time (R*C) is?
3. it seems that racing your hand towards the antenna can make the decay shorter?
Even though you don't use an explicit knee, I'm wondering if you are somehow (perhaps without realizing it) employing the non-linearity near the antenna? If I jack the velocity up on the prototype I can get it to "trigger" anywhere, but that also makes the volume field pretty twitchy.Thanks!
I am happily using a Sony RX100 M3.
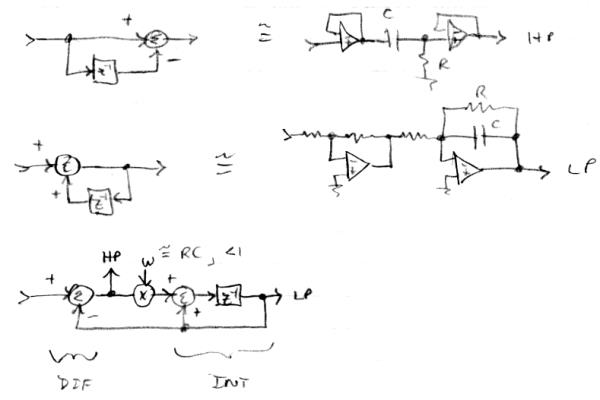
1. There is no diode. The 'bednarz-schaltung' (a friend called it so humorously) consists of an opamp, an electrolytic, six resistors and a potentiometer.
2./3. I have had to look it up again with a scope: decay behaves just like attack – velocity dependent. But the further away from the loop, the less velocity has an effect.
There are no fixed attack or decay events like in e.g. ADSR or AR or whatever envelope generators.
The non-linear positive or negative or zero acceleration of loudness is momentarily determined by the hands speed. Here i was writing:
- let A be the control voltage corresponding to the volume hands position.
- let B follow that voltage, but delayed. Like B'new=B'old+(A-B'old)/2
- A/B'new gives a multiplier to somehow generate the velocity voltage
I guess that was confusing.
Imagine you hold one end of a soft tension spring (let it be 20cm) in your hand. On the other end a somehow suited weight is being attached. If you slowly raise your arm, the distance between the hand and the weight won't differ. But a fast move up will stretch the spring in our example rapidly up to 60cm. While the weight after that move follows and settles smoothly in its normal position (in fact it would jump around wildly, but let our spring be a magic one). The lenght of the spring is the multiplier for the positive acceleration. Of course this example works for positive acceleration only.
I guess that was even more confusing.