Noise II
I'm re-reading Dattorro's excellent "Effects Design Part 3" paper in the course of taking another look at the LC oscillator dither generators. I realize now that my previous post on audio noise generation [LINK] has a glaring error, and I'd like to address that now. I made a spreadsheet (noise_2018-10-23.xls) if you want to really see what's going on and maybe play with it a little: [LINK]. Some notes from that:
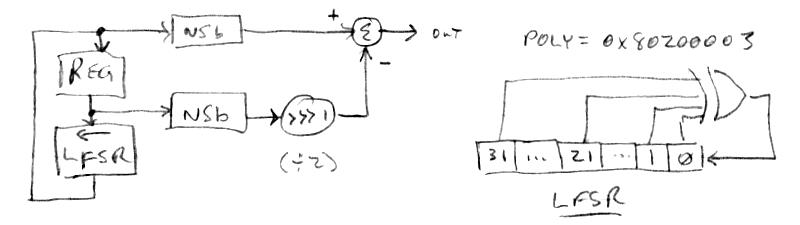
For computation, we want the whitest noise as fast as possible, and the most efficient algorithm I've run across is this one. The simplest way to do this is take the parallel output vector (bits) from a (generally wider) LFSR (linear feedback shift register) after cycling it multiple times. I haven't studied exactly how many cycles are requited to sufficient whiten the output, but it is definitely more than one. If we only do one cycle and the shift is left, each output value is often 2x the previous output (with an additional LSb=1 one half of the time). Thus the outputs are highly related to each other, and the FFT forms a roughly +10dB ramp from the highest to lowest frequency, so lower frequencies are somewhat emphasized. I won't go into Dattorro's derivation as it is extremely mathy and I can't say I follow it entirely, but the upshot is one can stick an exceedingly simple FIR filter on the output of a single cycle LFSR to flatten the FFT and thus whiten the noise. For such a simple seeming construct there are many ways to get things wrong and not get the expected result, so I'll spell them out explicitly here. The signal chain (elements described below) is: LFSR => NSB => FIR
The LFSR
Dattorro unfortunately doesn't come right out and say it, but I believe he is using a right shifted LFSR. The shift direction is important because I believe it determines the weightings in the whitening filter. Anyway, my code uses a left shifted LFSR, that is:
1. The input value is ANDed with the LSFR polynomial (which has ones only at the tap locations).
2. The result of (1) is bit reduction XORed (where odd bit count gives -1, even bit count gives 0).
3. The (untouched) input value is shifted left once.
4. The result of (2) is subtracted from the result of the result of (3), which gives us the output value.
The polynomial I'm using for a 32 bit wide LFSR is 0x80200003.
Unipoloar To Bipolar Conversion (NSB)
Dattorro shows proper and improper ways to convert a single ended or unipolar noise vector to bipolar signed, and quite honestly I'm at a bit of a loss as to how he defines things here. But I believe (because of simulation) the way he converts from unsigned (unipolar) to signed (bipolar) is by negating the MSb (most significant bit). Flipping the MSb this way is mathematically equivalent to subtracting 1/2 if the number is considered to be a fraction (as DSP processors generally do), or subtracting 2^(n-1) from an n bit-wide value. The processor I'm using has an opcode that does this: NSB (not sign bit).
The Whitening FIR Filter
So the output of a single cycle of the LFSR is converted to bipolar and presented to the whitening filter. The output of the whitening FIR filter Dattorro shows in his paper is simply the input minus a one cycle delayed version of the input multiplied by 2:
out(n) := in(n) - 2*in(n-1) (Dattorro)
Whereas, since I'm using a left shift LFSR, I've found I had to change it to the following filter in order for it to function correctly, which is the input minus a one cycle delayed version of the input divided by 2:
out(n) := in(n) - in(n-1)/2 (spreadsheet & prototype code)
It's perhaps not obvious, but the output values go right up to but don't exceed the binary bounds, which is great. I should stress that you need to look at actual values produced, as a slightly wrong method may give a non-white spectrum, or a white spectrum but with output values confined to output maximum & minimum.
The above is coded up and running on the prototype and behaving quite well. I can't hear any difference between it and the previous incorrect version, but the incorrect version was clearly outputting min/max levels as the sample level was visually (but not audibly) rhythmically pumping.
Dattorro is one sharp cookie, I wish my brain worked 1/2 as well as his, dude's some kinda supergenius. His bio from that paper:
Jon Dattorro is from Providence, RI. He trained as a classical pianist, attended the New England Conservatory of Music where he studied composition and electronic music, and performed as soloist with Myron Romanul and the Boston Symphony Orchestra for Children’s Concerts at Symphony Hall. His scores include a ballet and a piano concerto.
Mr. Dattorro received a B.S.E.E. with highest distinction from the University of Rhode Island in 1981, where he was a student of Leland B. Jackson. In 1984 he received an M.S.E.E. from Purdue University, specializing in digital signal processing under S. C. Bass. He is currently working towards a Ph.D. in electrical engineering at Stanford University.
He designed the Lexicon Inc. model 2400 Time Compressor with Charles Bagnaschi and Francis F. Lee in 1986, and he designed most of the audio effects from Ensoniq Corp. between 1987 and 1995. He shares two patents in digital signal processing chip design with David C. Andreas, J. William Mauchly, and Albert J. Charpentier. Personal mentors are Salvatore J. Fransosi, Pozzi Escot, and Chae T. Goh.