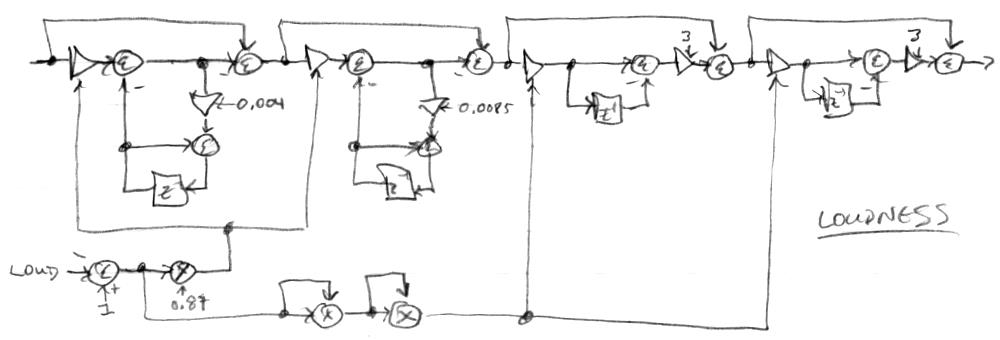
LOUDNESS!
Here's the analog loudness circuit from the article I pointed to yesterday:
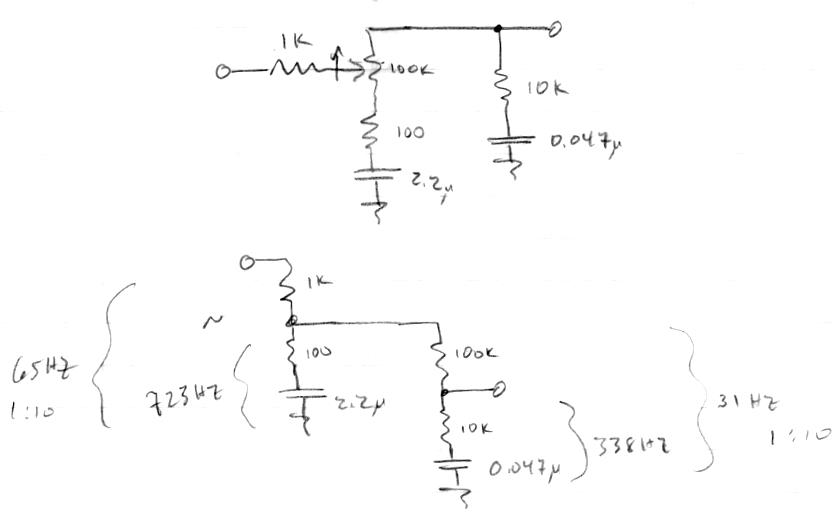
At top is the fairly clever circuit. Clearly, when the pot wiper is fully clockwise it's pretty much just a wire. At bottom is the equivalent circuit when the pot wiper is fully counter-clockwise and maximally "doing it's thing". Several things to note here:
1. It's a cascade of two first order low pass filters that can be considered to be isolated due to the 1:10:100 impedances.
2. The dual resistive dividers each individually limit the treble cut to 1:10 for a total of 1:100 or -40dB.
3. The treble cut limiting is a "shelving" action, so above some frequency the signal levels out.
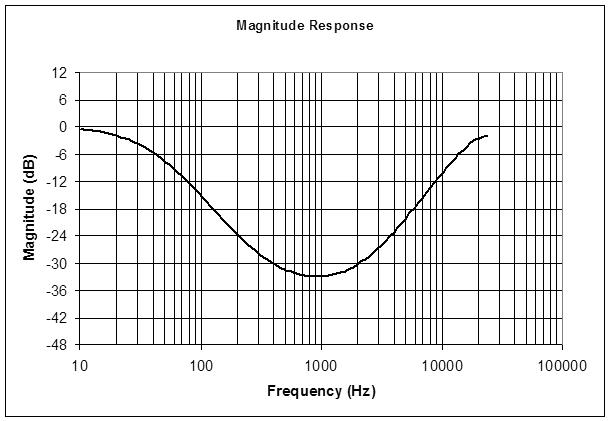
4. The -3dB cutoffs are at 65Hz and 31Hz, so signals roughly below 31Hz aren't attenuated.
5. The shelving points are 723Hz and 338Hz, so signals roughly above 723Hz are leveling out.
How to implement this digitally? Zölzer's book shows ways to use all-pass filters with feed-forward to create low and high pass filters, and mixing the filter input with the filter output creates a shelving filter. There are ways to use feed-back for cut, but they're hampered by the need for a delay (in order to be "causal") which messes with the response at the extremes. So feed-forward is the way to go here, and it conveniently gives us a [0:1) range cut input parameter. There's no need to implement the high pass filters as all-pass, I believe that's just a unifying concept in Zölzer's chapter, so we'll use the normal high/low pass construct. As in the analog case, we need to cascade two shelving high cut filters in order to obtain a wide enough range and steep enough attenuation:
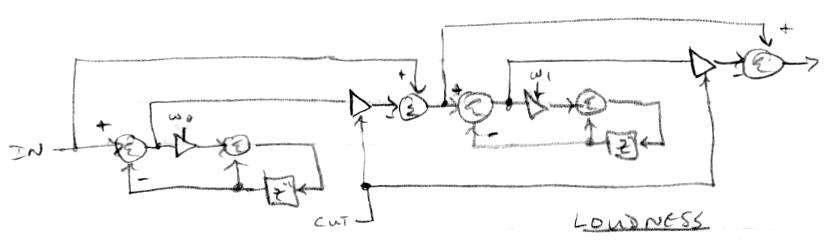
The cut input sense is reversed via the logical NOT operation so CW/CCW gives more/less treble, much like a conventional level control. And since there are two such attenuations in series, it seems a linear taper feels OK as the result is rather equivalent to a squared taper. The cut input is limited to 0.9 via extended multiplication (not shown here) so as to limit treble cut to -40dB. The construct is capable of doing a bit more than this but it gets pretty muddy down there. The frequency determining multiplications w0 and w1 are 0.004 and 0.0085 for -3dB @ 30.61Hz and 65.21Hz respectively, same as the analog case.
Here's the calculated response (Excel) when fully engaged:
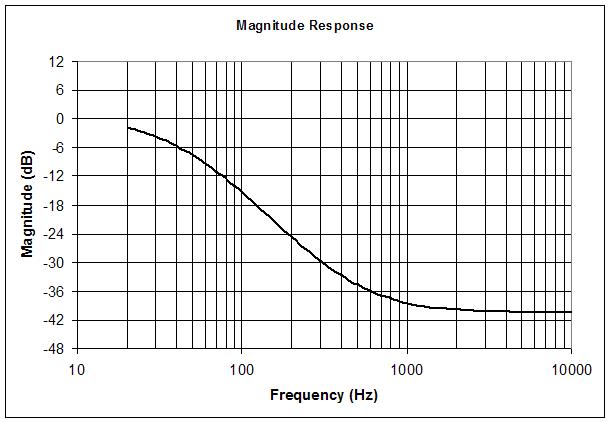
I've confirmed the above response on the prototype. Indeed, turning the loudness knob CCW lowers the overall volume without thinning out the bass.
Another audio / DSP mystery (for me, anyway) solved!