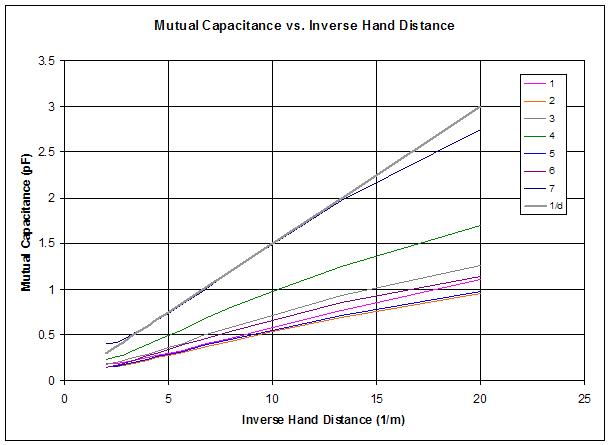
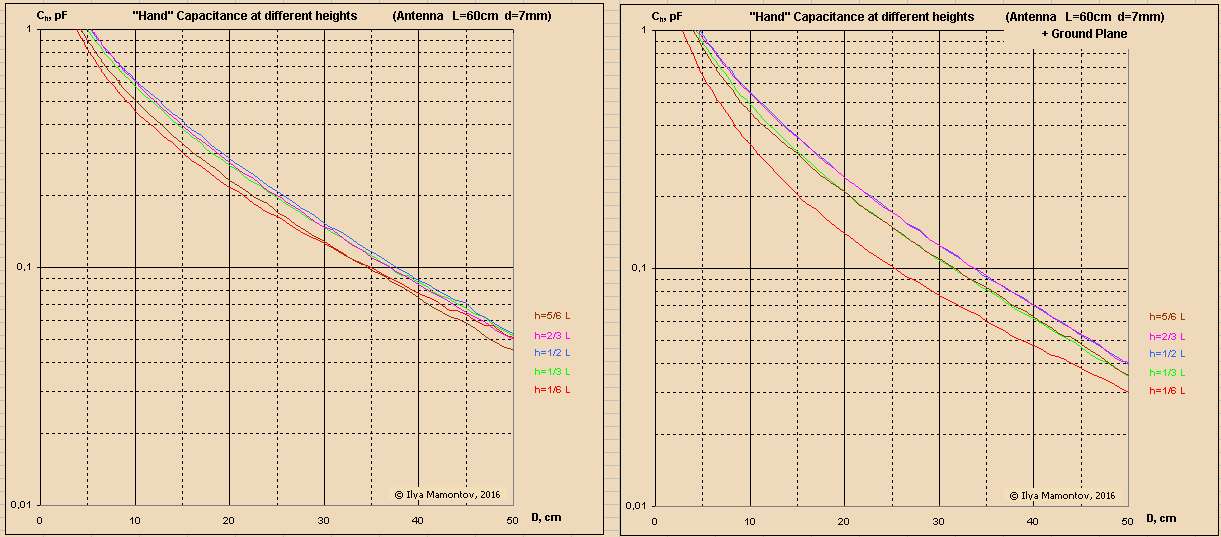
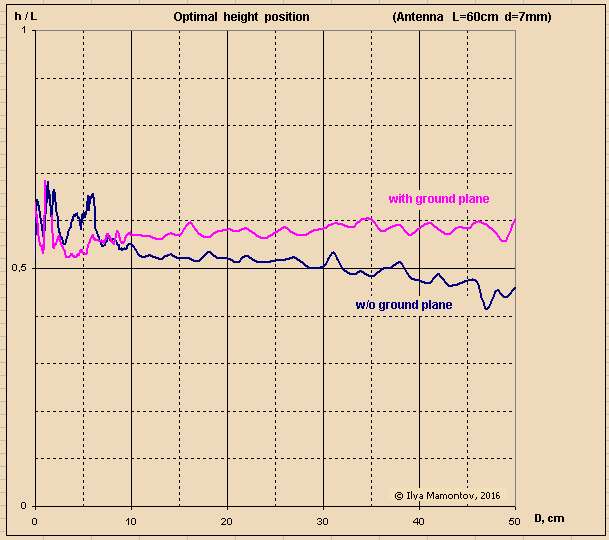
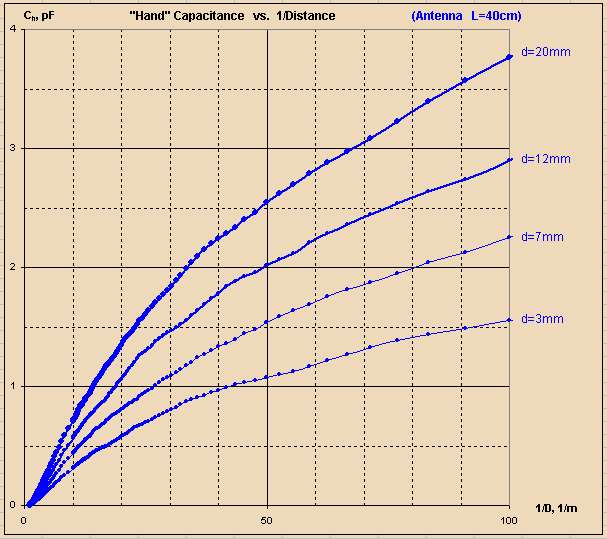
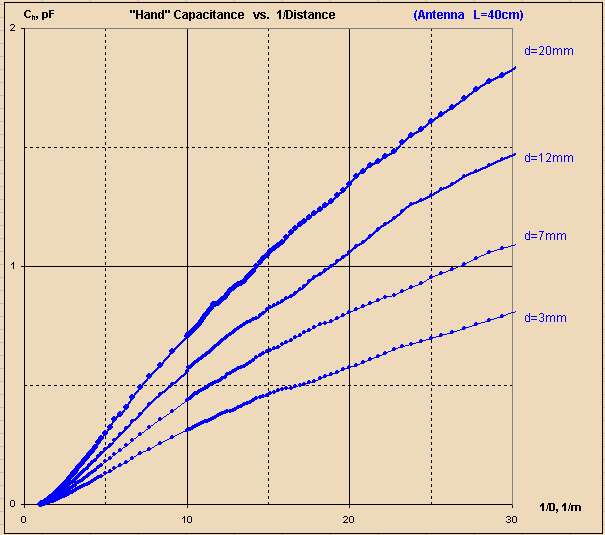
"More linear, but that's only a verification of the fact that sufficiently small segments of all curves can be considered as linear. MYTH: BUSTED" - ILYA
Yeah, no. I agree with your data (i.e. I haven't analyzed it, but it looks generally consistent with mine) but I disagree with your choice of presentation & your conclusion based on that.
My measurements with my real hand/arm/body were over a distance of 0.05m (~2") to 0.5m (~20").
The closest distance is about as close as I felt I could semi-accurately measure with the C getting pretty high and the frequency counter reading getting pretty squirrelly. I don't think an accomplished analog Theremin player would risk getting much closer to the antenna than this (unless they were doing it for effect - to make it squeal - and even then they generally want to avoid bumping the Theremin, and probably aren't super concerned about linearity of the squeal pitch, though non-linearity in this region probably causes some player anxiety).
The farthest distance is my arm and hand folded up next to my body so I literally couldn't get any farther away without moving my entire body (and I certainly didn't want to do that). Except for the presence of the motor, your setup doesn't seem to account for human body capacitance, and it doesn't really model a folding arm either. Without accounting for these things somehow you can't exactly definitively debunk data that was obtained with a real hand/arm/body. But, having said that, it's rather beside the point because I don't believe either of these are first order effects.
The corresponding 1/d for my measurements is 1/0.5 = 2 and 1/0.05 = 20. With these as the x-axis (i.e. 1/d) I reported some non-linearity on the small end of 1/d, presumably due to my arm folding into my body. For the rest I pretty much see your graph above going to 1/d = 20, which is strongly linear with 1/d, certainly better than any other numbers I've seen via heterodyning, offset heterodyning, period measurement, etc. and can be easily corrected via a mild polynomial if desired (I don't intend to).
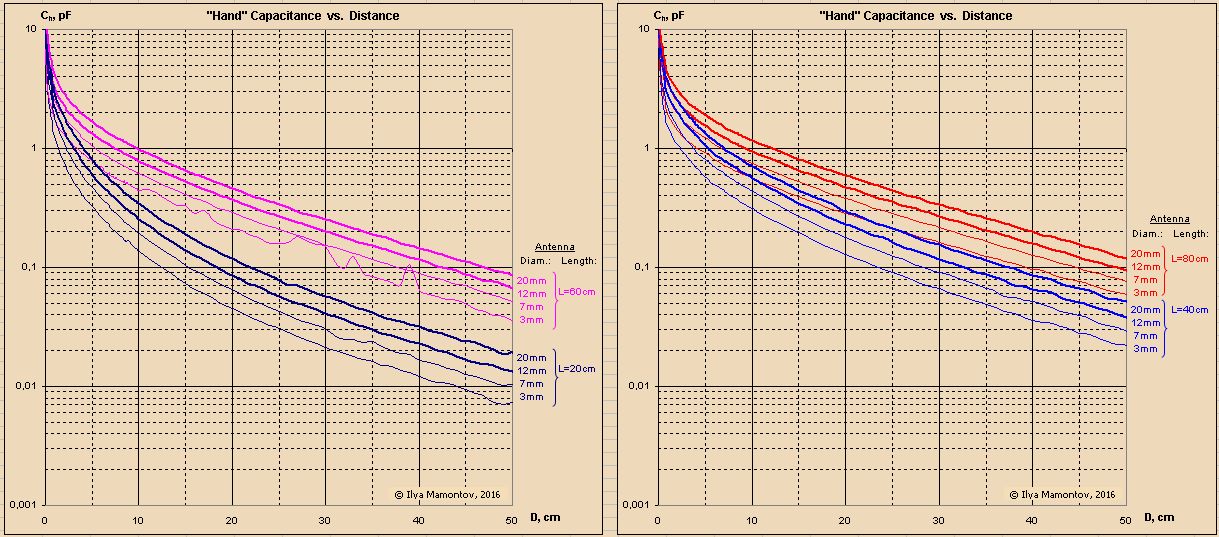
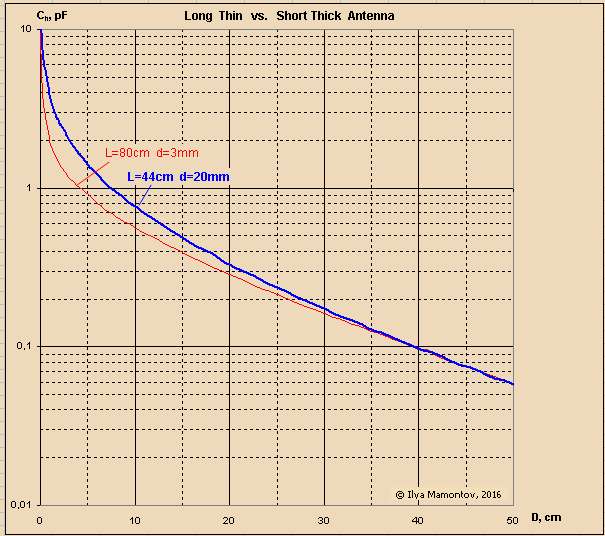
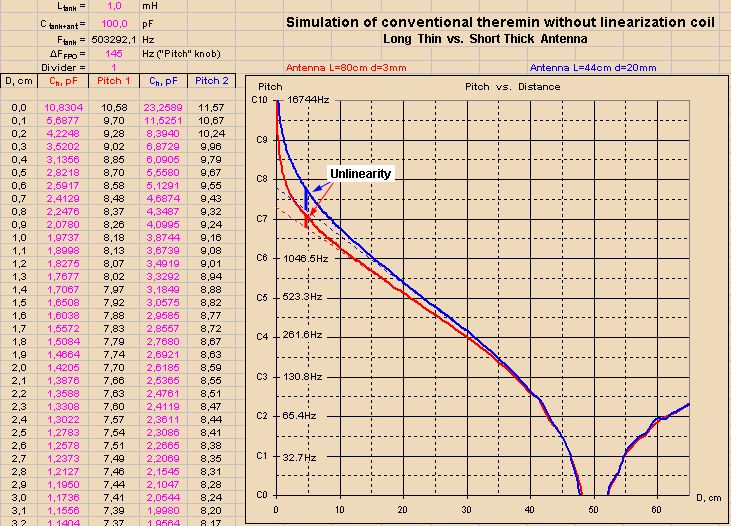
Your top graph goes to 1/d = 100, or d = 10mm. Your bottom graph goes to 1/d = 30, or d = 33.3mm. The difference in distance is minor, but the marked difference in the appearance of the graphs exaggerates non-linearity very close to the antenna (a region generally avoided when playing melodically). (Though this region on a digital Theremin that calculates back to 1/d should be much more playable than a heterodyning Theremin due to this mild drop, rather than rapid increase, in final pitch change right at the antenna.)
tldr: No real argument with your data, but the optics between your two graphs are very poor because the brain doesn't normally think in terms of 1/d.
ILYA: I'd like to see the results of a spherical hand and a plate antenna, this was the most linear (C vs. 1/d) and also the most sensitive in my simulations. Maybe use a 0.1m (4") diameter ball (styrofoam covered in aluminum foil) for the hand, and a 0.15m (6") x 0.3m (12") plate (aluminum flashing) for the antenna. Perhaps try both orientations of the plate since your arm model isn't super realistic. I'm not suggesting you do this experiment because I need any more proof (I'm convinced by my own experiments) but because it might be interesting for you and others.
And, as I've said before, I don't recommend using a rod shaped pitch antenna with digital Theremins. It will work and provide good linearity, but a plate will provide more linearity and much more sensitivity. My goal is to build the best Theremin possible, not necessarily the best looking Theremin in a traditional sense.